Explanation (which might be wrong, since I’m writing this after banging my head against a wall. Please do correct me if I’m wrong):

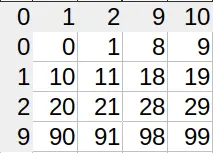
In regular numbering systems (i.e., decimal), we exhaust all 10 digits (0–9) before we reach two-digit numbers. The first number to require 3 digits is 10². The first to use 4 is 10³, and so on.

In music intervals, there is no “0”. The interval c’–c’, for instance, is called a prime (1). This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.

In Excel, shit hits the fan when you need to convert column names (A, B, C…) to numbers (0, 1, 2…). Since we use 26 characters as our ‘digits’, we’re in the hexavigesimal system. Knowing what I told you in the first paragraph, you’d expect the first double-digit column (AA) to be 26. And you’re right.

However, when do we need 3 digits? Which column is column AAA? A sane person would say it’s 26², so 676. Ha! No. Column number 676 is actually ZA. What gives? Well, we only ditch the zero for single digit numbers. All subsequent columns actually use 27 different characters, the ‘empty character’ being one of them. That’s where we get the ‘single digit’ – there actually is a second digit, only it’s empty.

So the column AAA actually has index 702, or 26×27. Which index does the column AAAA have? 26×27². The system of adding powers of the base works, only we changed bases midway through.

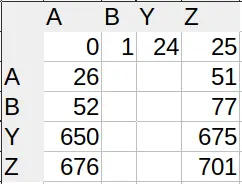
You can see the lopsidedness in the index lookup table (I’m not displaying all characters for brevity). Sane number systems have square tables. Excel’s is 26×27 (shown are 4×5).

  • Corvulus Morti@sh.itjust.worksEnglish
    13·
    1 day ago

    This is a very fun implicit question!

    First, in decimal, there are 10 symbols: 0-9. When we count from 0 to 9, the next number is 10, not 00 (which is equivalent to 0).

    In base 26, there are 26 symbols (A-Z). If one wanted to use these symbols in the same way, A would be equivalent to 0, so 26 is represented by BA, not AA. However, if AA is not the same as A, then we can represent 26 as AA instead of BA.

    Basically, in our typical numbering system, the leading digit can’t be 0, so there are 9×10 possible two digit numbers, and 10 possible single digit numbers. However, if the first digit can be 0, meaning, for example, if 03 is not the same as 3, there are 10×10 possible two digit numbers. This second approach is what excel and google sheets use. Column A is not the same as column AA. Hence, you start with single digit column numbers (A-Z). Then you move to two digit column numbers (AA-ZZ), of which there are 26². The last column before triple digits is column 26+26²=702. The first triple digit column number is 26+26²+1=703. Neat!

    Comparing this to our system, the first 2 digit number is 10¹=10. The first 3 digit number is 10²=100. The first 4 digit number is 10³=1000.